Сумма внешних углов многоугольника - важная геометрическая характеристика, которая имеет постоянное значение для любых выпуклых многоугольников независимо от количества сторон.
Содержание
Основная теорема о сумме внешних углов
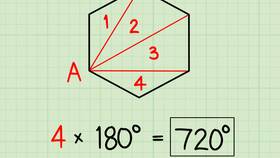
Для любого выпуклого n-угольника сумма внешних углов, взятых по одному при каждой вершине, равна 360°.
Математическое выражение
Σ внешних углов = 360°
где Σ - знак суммы, n - количество сторон (углов) многоугольника
Доказательство теоремы
- В каждой вершине многоугольника внешний и внутренний углы смежные
- Сумма смежных углов равна 180°: α + β = 180°
- Сумма внутренних углов n-угольника: Σα = (n - 2) × 180°
- Сумма всех смежных пар: Σ(α + β) = n × 180°
- Вычитая из этого сумму внутренних углов, получаем: Σβ = n × 180° - (n - 2) × 180° = 360°
Примеры для различных многоугольников
| Многоугольник | Количество сторон | Сумма внешних углов |
| Треугольник | 3 | 360° |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 360° |
| Шестиугольник | 6 | 360° |
Особые случаи
Для невыпуклых многоугольников
Теорема также верна для невыпуклых многоугольников, если внешние углы измеряются с учетом знака (положительные при повороте против часовой стрелки).
Для звездчатых многоугольников
Сумма внешних углов звездчатых многоугольников может отличаться от 360° и зависит от конкретной конфигурации.
Практическое применение
- В архитектуре при проектировании зданий
- В компьютерной графике при моделировании объектов
- В навигации и геодезии
- При решении геометрических задач на доказательство
Связь с суммой внутренних углов
Зная сумму внешних углов (360°), можно вычислить сумму внутренних углов: Σ внутренних углов = 180° × n - 360° = 180° × (n - 2)
Таким образом, сумма внешних углов любого выпуклого многоугольника всегда постоянна и равна 360°, что делает это свойство универсальным для всех правильных и неправильных выпуклых многоугольников.